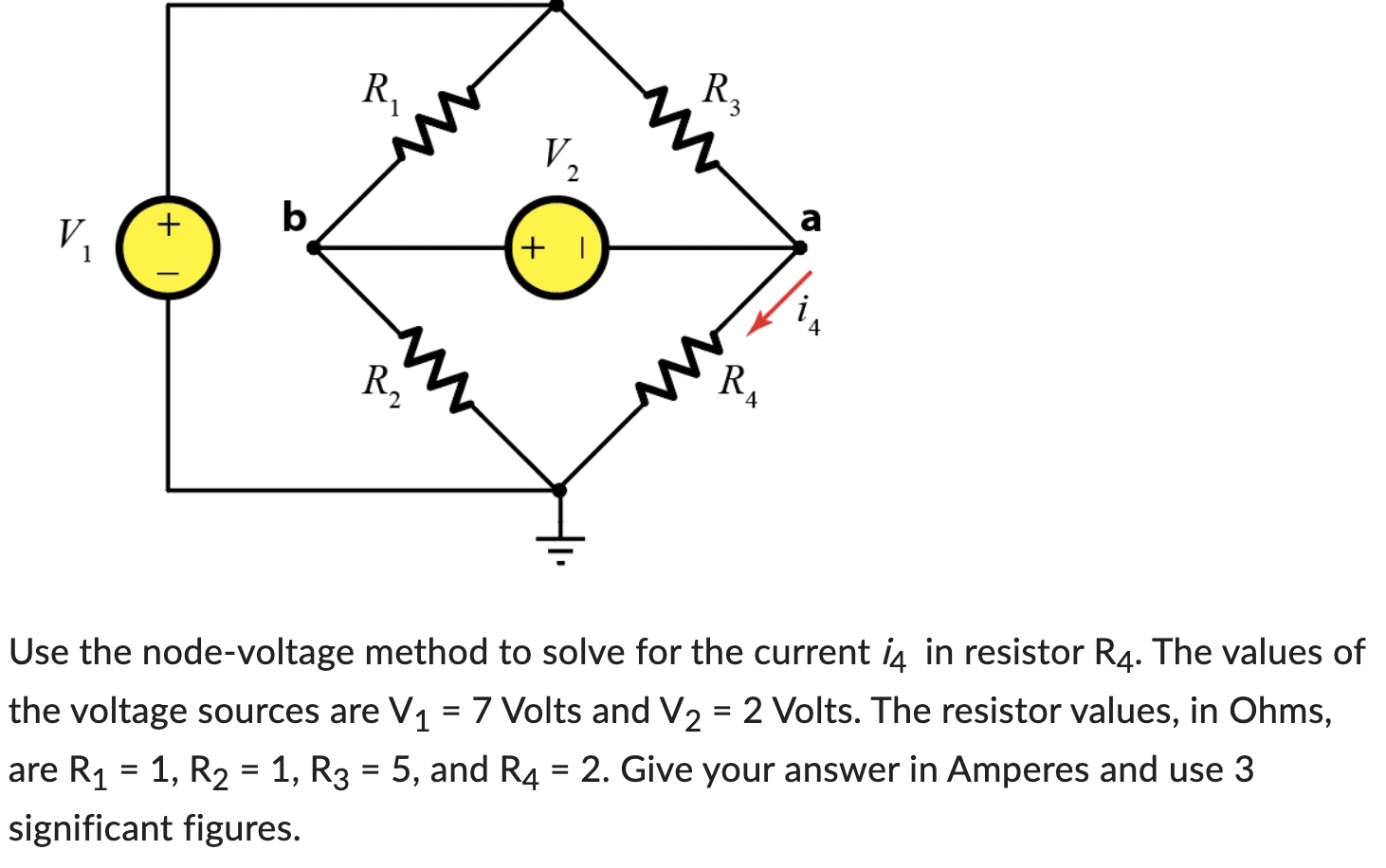
Nice Info About How To Do Node Voltage

Understanding Node Voltage Analysis

1. What Exactly is Node Voltage?

Ever looked at a circuit diagram and felt like you were staring at an alien language? Fear not! We're diving into node voltage analysis, a technique that helps you decipher those electronic hieroglyphs. Essentially, node voltage analysis is a way to find the voltage at different points (nodes) in a circuit. Think of it like finding the elevation at different points on a topographical map. Once you know the voltage at each node, you can easily calculate currents and power throughout the circuit. It's a fundamental tool in any electrical engineer's arsenal, and with a little practice, you'll be wielding it like a pro.

Why is this so important? Well, understanding the voltage at different points allows you to predict how the circuit will behave. Will that LED light up brightly? Will that motor spin at the correct speed? Node voltage helps you answer these questions before you even build the circuit, saving you time, money, and maybe even a few blown fuses. Plus, mastering node voltage gives you a solid foundation for tackling more advanced circuit analysis techniques down the road.

Before we get started, there's a few things we need to be aware of. A node, put simply, is a point in a circuit where two or more components are connected. The "reference node" is a specifically chosen node that all other voltages are measured with respect to. We usually designate this as "ground", and assign it 0 volts. Lastly, independent voltage and current sources provide a known voltage or current regardless of what is connected to them. These are our starting points!

So, buckle up, grab your calculator (or your favorite online circuit simulator), and let's get ready to unravel the mysteries of node voltage analysis. Prepare to feel like a circuit-solving superhero!

The Step-by-Step Process of Node Voltage Analysis

2. Identifying Nodes and Choosing a Reference Node

Okay, the first step is like scouting the territory before you build your fort. You need to identify all the nodes in your circuit. Remember, a node is any point where two or more components connect. Mark them clearly on your diagram. Now, here comes a crucial decision: choosing your reference node. The reference node, often called the "ground," is where you assign a voltage of 0V. Think of it as your baseline, the starting point from which you measure all other voltages. Generally, you want to choose a node with lots of connections, as this will simplify your calculations later on. If there's a ground symbol already in the schematic, then you are set!

A good way to visualize this is imagining a river system. Each node is a point on the river, and the water level at each point represents the voltage. Your reference node is like the sea level the point from which you measure the height of all other points on the river. Choosing a well-connected point as ground is like choosing the widest part of the river as your baseline - it helps streamline your analysis.

Don't stress too much about picking the "perfect" reference node initially. It's like choosing the best parking spot — sometimes, you just gotta pick one and go with it. If you find the math getting hairy later, you can always reconsider your choice. The important thing is to clearly identify your reference node and stick with it throughout your analysis.

Once you've identified all the nodes and selected your reference node, you're ready to move on to the next step: applying Kirchhoff's Current Law!

3. Applying Kirchhoff's Current Law (KCL)

Now, let's talk about Kirchhoff's Current Law, or KCL for short. This is the heart of node voltage analysis. KCL states that the total current entering a node must equal the total current leaving the node. Think of it like a water pipe junction: what flows in must flow out, or the pipe will burst! Mathematically, this means the sum of currents entering a node is zero. I like to think of this as a closed system, kind of like the water cycle.

For each node (except the reference node), you'll write an equation based on KCL. This involves expressing the current flowing through each component connected to the node in terms of the node voltages and the component's resistance (using Ohm's Law, V=IR, rearranged as I=V/R). You might be asking: How do I know which direction the current is flowing? Well, you can assume a direction. If your assumption is wrong, the current will just come out negative, so don't worry about getting it perfect on the first try!

Be careful with current sources! If a current source is connected to a node, the current it provides is already known. This simplifies the KCL equation for that node. But remember to account for the direction of the current source when setting up your equation. It's like having a pump in your water pipe system — you know exactly how much water it's pushing in (or pulling out).

After applying KCL to each node, you'll have a system of equations. The number of equations will be equal to the number of non-reference nodes. The next step is to solve these equations to find the node voltages. Think of solving these equations like solving a jigsaw puzzle. Each equation is a piece of the puzzle, and once you put them all together, you'll see the complete picture of the voltages in your circuit.

4. Solving the System of Equations

Alright, you've identified the nodes, chosen your reference, and meticulously applied KCL to generate a system of equations. Now comes the fun part: solving those equations! There are a few ways to tackle this. You can use substitution, elimination, or even matrix methods (if you're feeling fancy). Personally, I often use online equation solvers or circuit simulators to speed things up. But it's important to understand the underlying principles, even if you're using a tool to do the heavy lifting.

Substitution involves solving one equation for one variable and then substituting that expression into the other equations. Elimination involves adding or subtracting multiples of equations to eliminate one variable at a time. Matrix methods (like Gaussian elimination or Cramer's rule) are more systematic and efficient for larger systems of equations. Choose the method you're most comfortable with. And don't be afraid to double-check your work!

Pro-tip: Keep your equations organized! Write them neatly and label each variable clearly. This will help you avoid making mistakes and make it easier to track your progress. It's like organizing your toolbox before starting a big project — it saves you time and frustration in the long run.

Once you've solved the system of equations, you'll have the values of the node voltages. These are the voltages at each node relative to your reference node (ground). With these voltages in hand, you can now easily calculate other circuit parameters, such as currents and power dissipations.

Putting it All Together

5. Using Node Voltages to Find Currents

You've conquered the node voltages! Now, let's use this newfound knowledge to determine the currents flowing through each component in your circuit. This is where Ohm's Law (V = IR) comes back into play. Remember, Ohm's Law relates voltage, current, and resistance. If you know the voltage across a resistor and its resistance, you can easily calculate the current flowing through it using I = V/R.

To find the voltage across a resistor, simply subtract the voltage at one node connected to the resistor from the voltage at the other node. The direction of the current flow is from the higher voltage node to the lower voltage node. If you assumed the wrong direction initially, don't worry, the current will simply come out as a negative value, indicating that the current is flowing in the opposite direction.

For components other than resistors (like voltage sources or current sources), the current may be known or may need to be determined using other circuit analysis techniques. But for resistors, Ohm's Law provides a straightforward way to calculate the current once you know the node voltages.

Calculating these values is like building a bridge from the voltages you found earlier to the actual behaviour of the circuit, allowing you to understand how everything is interacting!

6. Calculating Power Dissipation

Alright, you know the voltages and currents, so let's talk about power. Power is the rate at which energy is transferred or consumed in a circuit. In a circuit, power is typically dissipated by resistors as heat. The power dissipated by a resistor can be calculated using the formula P = VI, where P is the power, V is the voltage across the resistor, and I is the current flowing through it. You can also express power in terms of resistance: P = I²R or P = V²/R.

When dealing with multiple resistors, you can calculate the power dissipated by each resistor individually and then sum them up to find the total power dissipated in the circuit. Understanding power dissipation is important for circuit design, as it helps you ensure that your components can handle the amount of power they're dissipating without overheating or failing.

Power sources, on the other hand, supply power to the circuit. The power supplied by a voltage source is equal to the voltage of the source multiplied by the current flowing out of the source. The power supplied by a current source is equal to the current of the source multiplied by the voltage across the source.

Understanding power dissipation is crucial for efficient design. If something is burning, you can calculate backwards using the method we have learned to potentially find the issue at hand!

Tips and Tricks for Mastering Node Voltage

7. Simplifying Circuits with Source Transformations

Want to make your node voltage analysis even easier? Consider using source transformations! A source transformation allows you to convert a voltage source in series with a resistor into an equivalent current source in parallel with a resistor (and vice versa). This can simplify your circuit and reduce the number of nodes you need to analyze. It's like swapping a bulky piece of furniture for a more streamlined one, making your room (or circuit) more spacious and manageable.

The key to source transformations is to ensure that the equivalent circuit provides the same voltage and current to the rest of the circuit as the original circuit. To convert a voltage source in series with a resistor into a current source in parallel with a resistor, the current of the current source is equal to the voltage of the voltage source divided by the resistance (I = V/R), and the resistor remains the same. The reverse transformation is similar.

Before applying source transformations, carefully consider whether it will actually simplify your circuit. Sometimes, it might make things more complicated. But in many cases, source transformations can be a powerful tool for streamlining your analysis.

With practice, source transformation can significantly speed up node voltage analysis! It makes it very easy to identify the main elements of the circuit, and work from there.

8. Dealing with Dependent Sources

Dependent sources (also called controlled sources) are sources whose voltage or current depends on another voltage or current in the circuit. These sources can make node voltage analysis a bit more challenging, but don't worry, you can handle them! The key is to carefully track the controlling voltage or current and express the dependent source's voltage or current in terms of that controlling variable.

When applying KCL to a node connected to a dependent source, be sure to include the dependent source's voltage or current in your equation, expressing it in terms of the controlling variable. This will introduce an additional equation into your system of equations, but it's necessary to properly account for the behavior of the dependent source.

Dependent sources are often used to model transistors and other active devices. So, understanding how to deal with them is essential for analyzing more complex circuits.

Dependent sources are the final boss for circuit analysis, so if you get to this point, feel proud! There are many guides for those particular components that can help you further your understanding.